\[P(N(t) = k) = \frac{e^{-λt}(λt)^k}{k!}\]
학부 때 배웠던 포아송 분포를 기억하는가?
N(t): 시간 t까지 발생한 이벤트 수
“특정 시간 간격 동안 사건의 수를 설명하는 분포”
- 1분 동안 콜센터에 몇 통의 전화가 올까?
- 하루 동안 웹사이트에 몇 명이 접속할까?
포아송 프로세스로 확장돼서, “시간이 흐르면서 사건이 언제 일어났는지를 모델링”하게 된다.
포아송 프로세스의 세 가지 성질
1) 시작은 0 -> N(0) = 0
2) independent increments
3) stationary increments
이렇게 되면 자연스럽게 \(N(t) \sim \text{Poisson}(λt)\)
각 increment: N(t+s) - N(t)가포아송을따름 -> N(t)도 포아송이고 increments도 포아송을따르게됨
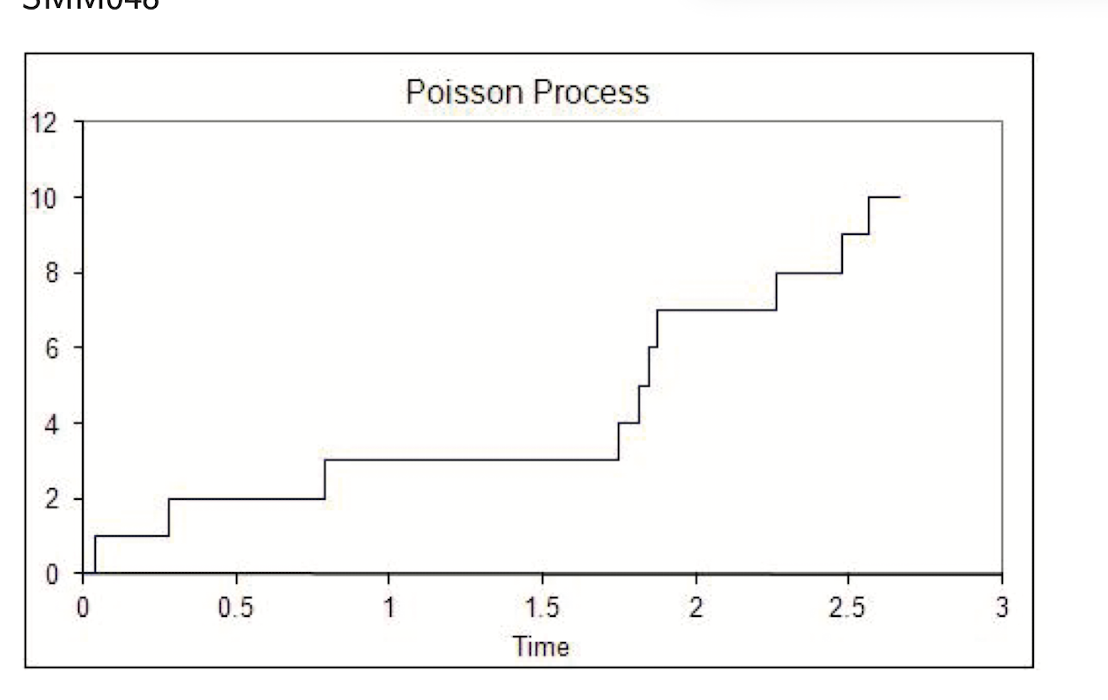
포아송프로세스의 성질
1) 아주작은 시간간격 dt동안 한 개의 사건이일어날 확률:
\[\mathbb{P}(N(t+dt) = j \mid N(t) = j-1) = \lambda dt + o(dt)\]
2) 사건이 안일어날확률
\[\mathbb{P}(N(t+dt) = j \mid N(t) = j) = 1-\lambda dt + o(dt)\]
아주 작은 dt동안에 두 개 이상의 사건이 일어날확률은 o(dt)로, 무시 가능할만큼작다.
'Stat' 카테고리의 다른 글
| Stochastic Process 마르코프성질 정상성 정상증가분 독립증가분 (2) | 2025.04.07 |
|---|---|
| Factor Analysis 요인분석 R로 해보기 (0) | 2024.10.27 |
| 충분통계량 (1) | 2023.12.10 |
| Exponential Family 지수족 (정규분포, 이항분포 증명) (1) | 2023.12.03 |
| Efficient Estimator 유효추정량 (0) | 2023.11.28 |



